Zo aan het eind van het jaar, vroeg me weer eens af of 1+1=2 wel 1+1=2 is.
Als je in de winkel komt en je vraagt mag ik 1+1=2 van u, dan zal al snel blijken dat je het niet kopen kunt.
Eigenlijk heb je er niks aan zonder dat je aangeeft wat je eigenlijk wilt kopen, je kun wel vragen mag ik 1 appel + 1 appel = 2 appels van u kopen, om het makkelijk te maken is men overgegaan om te vragen naar 2 appels.
Zo kun je ook 1 kilo appels kopen, maar 1 kilo is gelijk aan duizend, dus krijg je dan 1000 appels, in het geaccepteerde spreek verkeer is het gewoon dat u dan 1 kilo gram appels koopt.
Maar hoe zit het nu met 1+1=2, klopt dit wel?
Ik zoekt al een tijdje het bewijs dat 1+1 gelijk is aan 2.
Men heeft mij wel eens verteld dat er 10 bladzijden lang bewijs is geleverd.
Het lijk mij wel eens leuk het bewijs in handen te hebben want het kan een leuke discussie opleveren op een stille oudejaarsavond.
Want ik denkt dat zoiets ogenschijnlijk "eenvoudigs", vrij diep teruggaat naar de beginselen van een theorie.
Het zijn de axioma’s van Peano die de basis vormen voor de constructie van de natuurlijke getallen.
Hier een antwoord van Ask dr. Math, of hier een pagina uit Principia Mathematica van Russel, waar dit soort fundamenten werden behandeld.
Ik denkt dat het gesprek op oudejaarsavond al heel snel ander gesprek gaat worden.
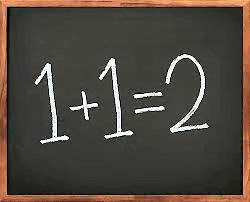

Stille oudejaarsavond. Die heb ik nog nooit meegemaakt. Ik had het vroeger nooit over rekenen, een geodriekhoek of de benen van een passer. Nee hoor, ik had het gewoon over de benen van ….. En dat waren me een benen. Daar kan ik het gerust een hele avond over hebben.
Love As Always
Di Mario